DLM模型
上一章我们介绍了ARIMA模型,这章我们来介绍DLM模型。在介绍DLM模型之前,首先谈一下状态空间模型(State space models)。状态空间模型将时间序列视为一个动态系统被随机扰动干扰的输出。它们将一个时间序列视为一些成分的组合,比如趋势,周期或者回归。
状态空间模型是在马尔科夫链(Markov chain)这样的相对简单独立结构的基础上,去为观察者定义更加复杂的模型。在一个状态空间模型中,我们假设有一个没有观察到的Markov chain,称为状态过程,时间序列是对不精确的估计。在工程应用中通常描述的是产生输出的物理观察系统的状态。另一方面,在计量经济学应用中通常是一个隐藏的结构,然而,通常有一个有用的解释。在任何一个例子中,可以把作为一个辅助的时间序列加速确定观察的时间序列的概率分布。
更加正式的说,一个状态空间模型包含一个维实数时间序列和一个维实数时间序列,满足下面的假设。
- 是一个马尔科夫链。
- 给定的条件,是独立的,并且只独立于。
基于上述两个假设,状态空间模型完全是由一个初始的分布和条件密度和。事实上,对于任意的,
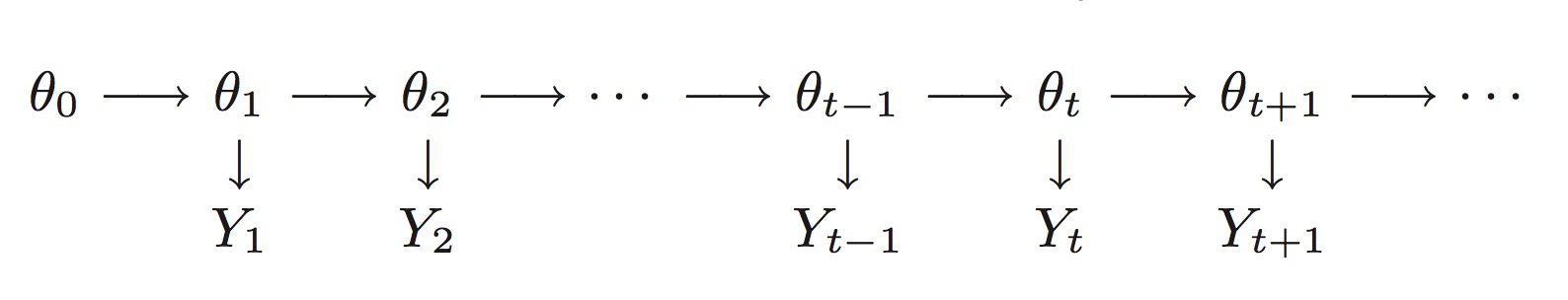
状态空间模型其中最重要的一类就是高斯线性状态空间模型,也叫做动态线性模型。动态线性模型其中最基础的部分,可以总结如下所示:
- 观察过程被认为是由隐状态加上高斯随机噪声决定的。如果我们知道连续时间点物体的位置,将是独立的:保留下来的仅仅是不可预测的测量误差。更多的是,仅仅依赖于时刻的位置。
- 隐过程有相当简单的动态性:不依赖于过去全部的轨迹,仅仅依赖于之前的位置,通过一个线性的关系加上高斯随机噪声。
- 评估和预测可以顺序的得到,当新数据可以获得的时候。
线性和高斯性的假设是针对动态线性模型(DLM)的,但是和的依赖结构是通用状态空间模型定义的一部分。
动态线性模型(DLM)是由一个在时间时刻p维状态向量的正态先验分布
和一对在任意时刻的状态和系统方程所定义。如下式所示:
下面介绍一些时间序列分析中的例子。对于单变量的时间序列,被称为随机噪声加上噪声模型,定义如下:
这里噪声序列和是独立的。
直观地,时间序列没有明显的趋势和季节变化是合适的:观察序列被建模为对一个水平上面的噪声观察,反过来,这一水平的变化又随着时间的变化而变化,由随机漫步所描述。这也是为什么这个模型被称为本地水平的模型。如果,就变成了常数平均模型。注意到随机漫步是非平稳的。的确,DLM可以用来对非平稳的时间序列进行建模。相反,通常的ARMA模型需要对数据做一个初始的变化来实现平稳性。
一个更加复杂的模型叫做线性增长模型,或者叫做局部线性趋势,其与局部水平模型有相同的观察方程,但是在动态性上面包含一个时变的坡。
状态估计和预测
状态空间模型广泛应用于应用问题的一个原因就是其灵活性。当然,就像在任何统计应用程序中一样,一个至关重要且常常困难的步骤是准确的模型定义。在很多问题中,统计学家和专家一起可以构建一个状态空间模型,其状态有一个直观的意义。专家知识可以用来指定状态方程中的转换概率,确定状态空间的维数等。但是创建模型通常比较困难。这里,我们假设模型已经给定,我们假设密度和已经给定,我们展示基础的回归用于估计和预测。
对于一个给定的状态空间模型,主要的任务就是对没有观察到的状态进行推断,或者基于观察序列的一部分预测未来的观察数据。根据已有的信息,通过计算感兴趣量的条件分布来解决估计和预测问题。
为了估计状态向量,我们计算了条件密度,我们区分了过滤问题,状态预测和状态平滑。值的强调的是过滤和平滑之间的区别。在过滤问题中,数据应该是按照顺序依次到达的。在DLM中,当新数据到达的时候,卡尔曼滤波器提供了公式去更新我们对状态向量当前的推断,将我们的过滤密度从到。平滑或者回溯分析的问题在于给定数据,评估在时间的状态序列。
事实上,在时间序列分析中,预测通常是主要的任务。状态估计仅是预测未来观察值的一个步骤;状态估计仅仅是预测未来观察值的一步。