激活函数的性质
- 非线性: 即倒数不是常数,是为了保证多层网络不会退化成单层线性网络。
- 几乎处处可微: 可微性保证了在优化中的梯度的可计算性。
- 计算简单: 激活函数在神经网络前向的计算次数与神经元的个数成正比,因此简单的非线性函数自然更适合用作激活函数。
- 非饱和性(saturation): 饱和指的是在某些区间梯度接近于零(梯度消失),使得参数无法继续更新的问题。eLU在x>0时导数恒为1,因此对于再大的正值也不会饱和。但同时对于x<0,其梯度恒为0,这时候它也会出现饱和的现象(在这种情况下通常称为dying ReLU)。Leaky ReLU和PReLU的提出正是为了解决这一问题。
- 单调性(monotonic): 单调性使得在激活函数处的梯度方向不会经常改变,从而让训练更容易收敛。
- 输出范围有限: 有限的输出范围使得网络对于一些比较大的输入也会比较稳定。
- 接近恒等变换(identity): 即约等于x,这样的好处是使得输出的幅值不会随着深度的增加而发生显著的增加,从而使网络更加的稳定,同时梯度也能够更容易地回传。
- 参数少: 大多数激活函数是没有参数的。
- 归一化: 这个是最近才出来的概念,对应的激活函数是SELU,主要思想是使样本分布自动归一化到零均值、单位方差的分布,从而稳定训练。在这之前,这种归一化的思想也被用于网络结构的设计,比如Batch Normalization。
Sigmoid和tanh
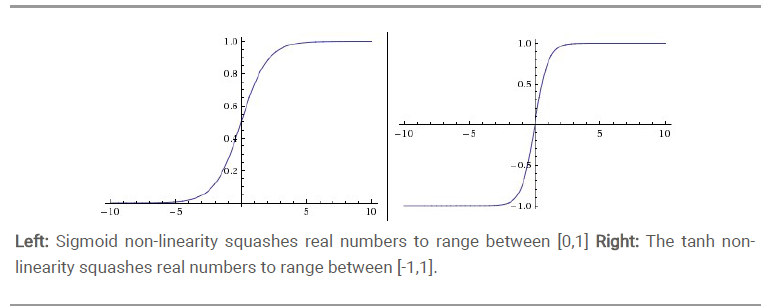
Sigmoid是常用的非线性的激活函数,上图中的左图,把连续实值压缩到0到1之间。数学形式如下:
主要有一些缺点:
- 梯度消失
- 输出均值不是0
tanh是上图中的右图,实际上,tanh是sigmoid的变形。与sigmoid不同的是,tanh是以0为均值的。
ReLU
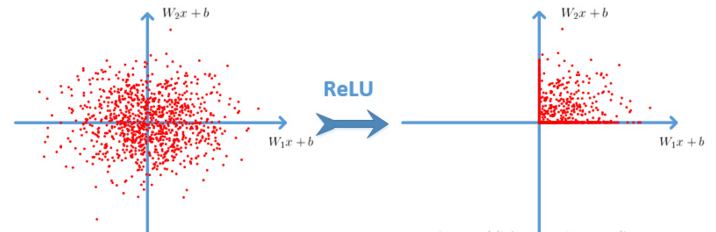
relu的数学公式如下。w是二维的时候,使用ReLU之后的效果如下:
Leaky-ReLU
Leaky-ReLU是用来解决”dying ReLU”的问题。定义如下:
这里的是一个很小的常数。这样,既修正了数据分布,又保留了一些负轴的值,使得负轴的值不会全部丢失。