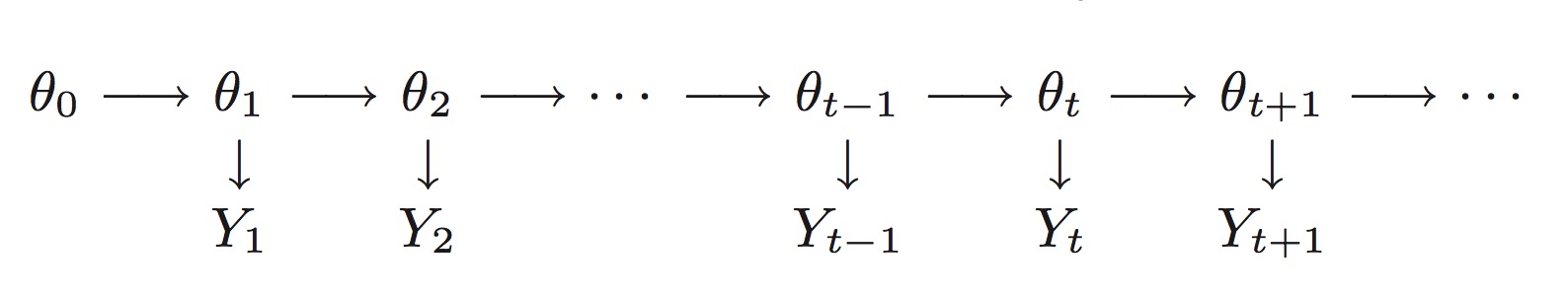DLM模型

  上一章我们介绍了ARIMA模型，这章我们来介绍DLM模型。在介绍DLM模型之前，首先谈一下状态空间模型(State space models)。状态空间模型将时间序列视为一个动态系统被随机扰动干扰的输出。它们将一个时间序列视为一些成分的组合，比如趋势，周期或者回归。

  状态空间模型是在马尔科夫链(Markov chain)这样的相对简单独立结构的基础上，去为观察者定义更加复杂的模型。在一个状态空间模型中，我们假设有一个没有观察到的Markov chain$\left( { \theta }_{ t } \right)$，称为状态过程，时间序列${ Y }_{ t }$是对${ \theta }_{ t }$不精确的估计。在工程应用中${ \theta }_{ t }$通常描述的是产生输出${ Y }_{ t }$的物理观察系统的状态。另一方面，在计量经济学应用中${ \theta }_{ t }$通常是一个隐藏的结构，然而，通常有一个有用的解释。在任何一个例子中，可以把$\left( { \theta }_{ t } \right)$作为一个辅助的时间序列加速确定观察的时间序列$\left( { Y }_{ t } \right)$的概率分布。

  更加正式的说，一个状态空间模型包含一个$p$维实数时间序列$\left( { \theta }_{ t }:t = 0,1,\cdots \right)$和一个$R$维实数时间序列$\left( { Y }_{ t }:t = 0,1,\cdots \right)$，满足下面的假设。

1. $\left( { \theta }_{ t } \right)$是一个马尔科夫链。
2. 给定$\left( { \theta }_{ t } \right)$的条件，${ Y }_{ t }$是独立的，并且只独立于${ \theta }_{ t }$。

  基于上述两个假设，状态空间模型完全是由一个初始的分布$\pi \left( { \theta }_{ 0 } \right)$和条件密度$\pi \left( { { \theta }_{ t } }/{ { \theta }_{ t-1 } } \right)$和$\pi \left( { { y }_{ t } }/{ { \theta }_{ t } } \right) , t\ge 1$。事实上，对于任意的$t > 0$，

$\pi \left( { \theta }_{ 0:t },{ y }_{ 1:t } \right) =\pi \left( { \theta }_{ 0 } \right) \cdot \prod _{ j=1 }^{ t }{ \pi \left( { { \theta }_{ j } }/{ { \theta }_{ j-1 } } \right) } \pi \left( { { y }_{ j } }/{ { \theta }_{ j } } \right)$

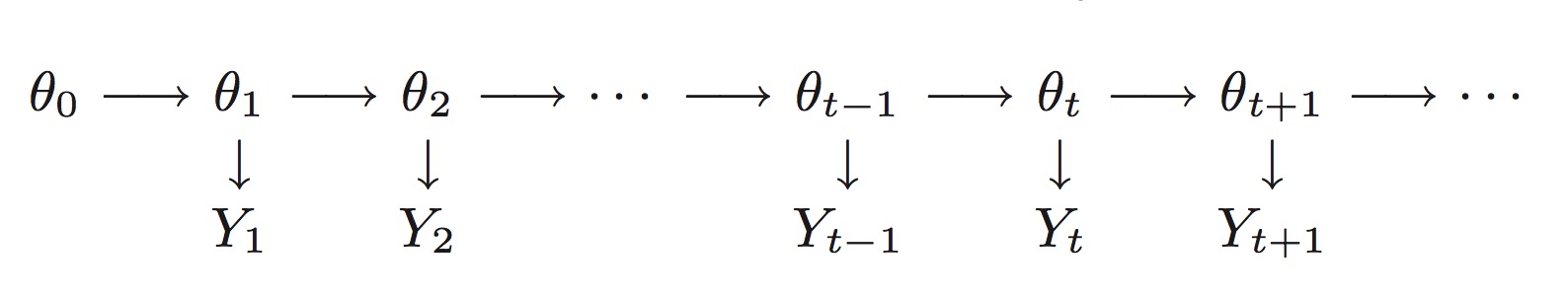
  状态空间模型其中最重要的一类就是高斯线性状态空间模型，也叫做动态线性模型。动态线性模型其中最基础的部分，可以总结如下所示:

• 观察过程$\left( { Y }_{ t }:t = 0,1,\cdots \right)$被认为是由隐状态$\left( { \theta }_{ t }:t = 0,1,\cdots \right)$加上高斯随机噪声决定的。如果我们知道连续时间点物体的位置，${ Y }_{ t }$将是独立的:保留下来的仅仅是不可预测的测量误差。更多的是，${ Y }_{ t }$仅仅依赖于$t$时刻的位置${ \theta }_{ t }$。
• 隐过程$\left( { \theta }_{ t } \right)$有相当简单的动态性:${ \theta }_{ t }$不依赖于过去全部的轨迹，仅仅依赖于之前的位置${ \theta }_{ t-1 }$，通过一个线性的关系加上高斯随机噪声。
• 评估和预测可以顺序的得到，当新数据可以获得的时候。

线性和高斯性的假设是针对动态线性模型(DLM)的，但是$\left( { Y }_{ t } \right)$和$\left( { \theta }_{ t } \right)$的依赖结构是通用状态空间模型定义的一部分。

动态线性模型(DLM)是由一个在时间$t=0$时刻p维状态向量的正态先验分布

${ \theta }_{ 0 }\sim { N }_{ p }\left( { m }_{ 0 },{ c }_{ 0 } \right)$

和一对在任意$t\ge 1$时刻的状态和系统方程所定义。

趋势项

周期项